みんなの量子コンピュータ
Chris Bernhardt 著
湊 雄一郎 翻訳
中田 真秀 翻訳
湊 雄一郎 監修
中田 真秀 監修
- 形式:
- 書籍
- 発売日:
- 2020年01月24日
- ISBN:
- 9784798163574
- 定価:
- 3,520円(本体3,200円+税10%)
- 仕様:
- A5・256ページ
- カテゴリ:
- プログラミング・開発
- キーワード:
- #プログラミング,#開発環境,#開発手法,#Web・アプリ開発
量子コンピューティングに関する基礎理論の全体像
【本書の内容】
本書は、量子ビットを使用したコンピューティングの数学的構造をわかりやすく紹介しています。
解説を単純化すると、量子状態に実際の係数のみを使用することで、位相の複雑さを軽減し、
初学者にもイメージしやすくしています。
一読すれば、すぐにでも量子コンピュータのエキスパートに近づけるという書籍ではありませんが、
量子コンピュータを形作る数学・物理学、アルゴリズム、論理回路など、多方面のアイデアと、
その源泉に触れることができます。
そのため、読者が直感的に理解している分野に関しては、その厳密なバックボーンを提供し、
理解の促進(あるいは取っ掛かり)が得られるはずです。
本書は、「なんとなく」や「話のタネ的に」ではなく、
量子コンピュータをベースに世界を構築したい人たちのための、最初の一冊です。
本書は
"Quantum Computing for Everyone" Chris Bernhardt
The MIT Press Cambridge
の翻訳です。
【本書のポイント】
・スピンやキュービット、スイッチなどの厳密な解説
・もつれ状態の構築実際の係数を使用して説明
・論理回路とユニバーサルゲートの構築法
・NP問題に適応する量子アルゴリズムの構築
【読者が得られること】
・量子コンピュータに必要な数学的背景
・80年代から続くアイデアの整理と展望
・高次コンピュータサイエンスの理解
【対象読者】
・理工学部学生
・量子コンピュータをターゲットとするエンジニア
・量子コンピュータ科学者
【著者について】
・Chris Bernhardt(クリス・バーンハルト)
Warwickユニバーシティで数学の博士号を取得後、Fairfieldユニバーシティの数学教授。
主な著述はコンピュータ理論であり、数学や物理、コンピュータ・サイエンスを含む分野がメインである。
この分野は、多くの美しく直感に反するアイデアが含まれており、
バーンハルト教授の目的は、すべてをできるだけシンプルにすることで、
非専門家にもこれらの重要なポイントを紹介することにある。
第1章 スピン
1.1 量子時計
1.2 同じ方向での測定
1.3 さまざまな方向での測定
1.4 測定
1.5 ランダム性
1.6 光子と偏光
1.7 まとめ
第2章 線形代数
2.1 複素数と実数について
2.2 ベクトル
2.3 ベクトル図
2.4 ベクトルの長さ
2.5 スカラーの乗算
2.6 ベクトルの加算
2.7 直交ベクトル
2.8 ブラとケットの積
2.9 ブラケットと長さ
2.10 ブラケットと直交性
2.11 正規直交基底
2.12 基底ベクトルの線形結合としてのベクトル
2.13 順序付き基底
2.14 ベクトルの長さ
2.15 行列
2.16 行列計算
2.17 直交およびユニタリ行列
2.18 線形代数の解法テクニック
第3章 スピンと量子ビット
3.1 確率
3.2 量子スピンの数学
3.3 等価な状態ベクトル
3.4 与えられたスピン方向に対応する基底
3.5 実験装置を60度回転させる
3.6 光子の偏光を表す数学モデル
3.7 特定の偏光方向に対応する基底
3.8 偏光フィルターの測定
3.9 量子ビット
3.10 アリスとボブとイブ
3.11 確率振幅と干渉
3.12 BB84プロトコル
第4章 量子もつれ
4.1 もつれのない量子ビット
4.2 もつれのない量子ビット計算
4.3 もつれた量子ビットの計算
4.4 超光速通信
4.5 テンソル積の標準基底
4.6 量子ビットをどうやってもつれさせるか
4.7 CNOTゲートで量子ビットをもつれさせる
4.8 もつれた量子時計
第5章 ベルの不等式
5.1 異なる基底でのもつれた量子ビット
5.2 もつれた状態を(|b0>,|b1>)で書き直す
5.3 アインシュタインと局所現実性
5.4 アインシュタインと隠れ変数
5.5 もつれ状態の古典的な説明
5.6 ベルの不等式
5.7 量子力学的モデルでの答え
5.8 古典的モデルでの答え
5.9 測定
5.10 量子鍵配送のためのエッカートプロトコル
第6章 古典論理、ゲート、および回路
6.1 論理
6.2 ブール代数
6.3 ゲート
6.4 回路
6.5 普遍的なゲート、NAND
6.6 ゲートと計算
6.7 メモリ
6.8 可逆ゲート
6.9 ビリヤードボールコンピューティング
第7章 量子ゲートと回路
7.1 量子ビット
7.2 CNOTゲート
7.3 量子ゲート
7.4 1つの量子ビットに作用する量子ゲート
7.5 完全な量子ゲートは存在するか
7.6 量子複製不能定理
7.7 量子計算と古典的計算
7.8 ベル回路
7.9 超高密度符号化
7.10 量子テレポーテーション
7.11 エラー訂正
7.12 コードの繰り返し
7.13 量子ビットフリップ補正
第8章 量子アルゴリズム
8.1 複雑性クラスPとNP
8.2 量子アルゴリズムと古典アルゴリズムの速度
8.3 クエリの複雑さ
8.4 ドイッチのアルゴリズム
8.5 アダマール行列のクロネッカー積
8.6 ドイッチ-ジョサのアルゴリズム
8.7 サイモンのアルゴリズム
8.8 複雑さのクラス
8.9 量子アルゴリズム
第9章 量子コンピューティングの与える影響
9.1 ショアのアルゴリズムと暗号解読
9.2 グローバーのアルゴリズムとデータ検索
9.3 化学とシミュレーション
9.4 ハードウェア
9.5 量子アニーリング
9.6 量子超越性と並行宇宙
9.7 計算
お問い合わせ
内容についてのお問い合わせは、正誤表、追加情報をご確認後に、お送りいただくようお願いいたします。
正誤表、追加情報に掲載されていない書籍内容へのお問い合わせや
その他書籍に関するお問い合わせは、書籍のお問い合わせフォームからお送りください。
利用許諾に関するお問い合わせ
本書の書影(表紙画像)をご利用になりたい場合は書影許諾申請フォームから申請をお願いいたします。
書影(表紙画像)以外のご利用については、こちらからお問い合わせください。
現在表示されている正誤表の対象書籍
書籍の種類:紙書籍
書籍の刷数:全刷

書籍によっては表記が異なる場合がございます
本書に誤りまたは不十分な記述がありました。下記のとおり訂正し、お詫び申し上げます。
対象の書籍は正誤表がありません。
| ページ数 | 内容 | 書籍修正刷 | 電子書籍訂正 | 発生刷 | 登録日 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 010 本文上から3行目 |
|
2刷 | 済 | 1刷 | 2020.03.02 | ||||||
| 016 本文下から2行目 |
|
未 | 未 | 1刷 | 2020.03.02 | ||||||
| 046 本文上から3行目 |
|
2刷 | 済 | 1刷 | 2020.03.02 | ||||||
| 046 本文上から5行目 |
|
2刷 | 済 | 1刷 | 2020.03.02 | ||||||
| 069 本文4行目から5行目 |
|
2刷 | 済 | 1刷 | 2020.03.02 | ||||||
| 072 本文最下行数式 |
|
2刷 | 済 | 1刷 | 2020.03.02 | ||||||
| 083 83ページ数式の下、「実際、各ペアが」から84ページ下から14行目までの4段落 |
|
未 | 未 | 2刷 | 2022.10.31 | ||||||
| 090 上から7行目の数式 |
|
未 | 未 | 1刷 | 2020.08.07 | ||||||
| 094 脚注5 |
|
2刷 | 済 | 1刷 | 2020.03.02 | ||||||
| 102 本文下から2行目 |
|
2刷 | 済 | 1刷 | 2020.03.02 | ||||||
| 102 脚注12 |
|
2刷 | 済 | 1刷 | 2020.03.02 | ||||||
| 177 脚注4 |
|
2刷 | 済 | 1刷 | 2020.03.02 | ||||||
| 182 本文上から8行目 |
|
未 | 未 | 1刷 | 2021.10.05 | ||||||
| viii 本文上から4行目 |
|
未 | 未 | 1刷 | 2023.01.24 |
mit さん
2022-02-18
日本語訳に意味不明なところが多くめげそうになるが、計算結果を頭で追っていけば著者の意図は理解できると思う。大学1年生レベルの数学が理解できれば、量子ゲート、量子アルゴリズムのこころを理解するための最初の一冊としてお勧め。
テキィ さん
2021-05-29
数式までは読めなかった
sumiyaki さん
2020-03-09
■コンパクトにまとまっていて大部ではなく読みやすい。数式があるものの、最初は簡単な線形代数学なので、前半の数式はついていけた。量子の世界の基本も説明されていて、入門書としてはとても良い。■誤植や文章のおかしいところが多少残っているので、正誤表が役に立つかも。参考図書の紹介のようなものがないのが残念。■量子コンピュータはかなり難しいものであり、アルゴリズムを開発するのは、私には難しそう。■個人的には「可逆ゲート」「可逆計算」というのが気になった。それがどう量子計算に関わるのかよく分からなかった。



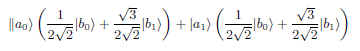
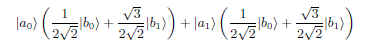
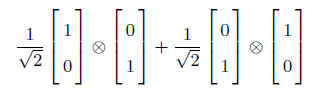
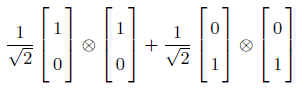


.png)

