暗号技術のすべて（IPUSIRON）｜翔泳社の本
  1. ホーム >
  2. 書籍 >
  3. 暗号技術のすべて

暗号技術のすべて

著

形式：
書籍
発売日：
ISBN：
9784798148816
定価：
3,850円（本体3,500円＋税10%）
仕様：
A5・720ページ
カテゴリ：
ネットワーク・サーバ
キーワード：
#ネットワーク・サーバ・セキュリティ,#データ・データベース,#システム運用,#Web・アプリ開発
紙の書籍
電子書籍

購入はこちら

企業・教育機関での一括購入

『ハッカーの学校』の著者が徹底解説
暗号技術の絡み合いを解き明かす

【本書のポイント】
1）古典暗号から現代暗号までを体系的に解説
2）アルゴリズムに注目することで、暗号技術の絡み合いを解き明かす
3）図や数値例を多数掲載し、数学も克服できるように配慮
4）教科書として、辞書として……いろいろな読み方ができる

【本書のねらい】
・「読める」…専門書や論文を読む準備ができる。
・「使える」…適切な運用や実装ができる。
・「見える」…日常に隠された暗号技術に気付く。
・「楽しむ」…古典暗号と現代暗号に魅了される。

【必要な予備知識】
・コンピュータの基礎知識
・高校レベルの数学知識（復習のための解説あり）

【内容紹介】
現代で安全な情報のやり取りをするには
暗号技術が不可欠です。

本書では、仕組みの説明だけでなく、
安全性や危険性について、利用する側と
攻撃する側の両面から見ていきます。

特にシステムの設計者や開発者が
正しく暗号技術を使えるように、
実装と運用の観点も加えました。

攻撃が成功するロジックや、
暗号化と復号の計算などを
自分で考える項目も用意しています。
ぜひ挑戦してみてください。

【ダウンロード特典あり】
本書をお買い上げの方に、ページ数の都合で泣く泣くカットした内容をまとめたPDF（約60ページ）をダウンロード提供しています。（詳しくは本書をお読みください）

【著者について】
IPUSIRON（イプシロン）
2008年情報セキュリティ大学院大学情報セキュリティ研究科情報セキュリティ専攻修士課程修了。以後、業務アプリなどの設計・開発、スマホアプリやWebアプリの検査・デバッグ、機械警備・防災設備の設置に従事。現在、情報セキュリティと物理的セキュリティを総合的な観点から調査しつつ、執筆を中心に活動中。主な書著に『ハッカーの学校』シリーズ（いずれもデータハウス）がある。

【目次】
第1章　情報セキュリティと暗号技術
第2章　古典暗号
第3章　共通鍵暗号
第4章　公開鍵暗号
第5章　ハッシュ関数
第6章　メッセージ認証コード
第7章　デジタル署名
第8章　鍵と乱数
第9章　その他の暗号トピック（ゼロ知識証明プロトコル、秘密分散共有法、電子透かし、SSL、OpenSSL、ビットコイン）

●CHAPTER 1　セキュリティと暗号技術
1.1　情報セキュリティの構成要素
1.2　セキュリティを実現する暗号技術
1.3　暗号技術のアルゴリズムを意識する

●CHAPTER 2　古典暗号
2.1　古典暗号の概要
2.2　シーザー暗号
2.3　コード
2.4　スキュタレー暗号
2.5　転置式暗号
2.6　単一換字式暗号
2.7　多表式暗号

●CHAPTER 3　共通鍵暗号
3.1　古典暗号から現代暗号へ
3.2　共通鍵暗号の概要
3.3　共通鍵暗号の定義
3.4　共通鍵暗号の仕組み
3.5　共通鍵暗号の安全性
3.6　共通鍵暗号の分類
3.7　バーナム暗号
3.8　ストリーム暗号
3.9　ブロック暗号
3.10　〈ブロック暗号〉DES
3.11　〈ブロック暗号〉トリプルDES
3.12　〈ブロック暗号〉AES
3.13　ブロック暗号の利用モード
3.14　〈暗号化モード〉ECBモード
3.15　〈暗号化モード〉CBCモード
3.16　〈暗号化モード〉CFBモード
3.17　〈暗号化モード〉OFBモード
3.18　〈暗号化モード〉CTRモード

●CHAPTER 4　公開鍵暗号
4.1　公開鍵暗号の概要
4.2　公開鍵暗号の定義
4.3　公開鍵暗号の安全性
4.4　公開鍵暗号に対する攻撃
4.5　RSA暗号
4.6　ElGamal暗号
4.7　一般ElGamal暗号
4.8　Rabin暗号
4.9　RSA-OAEP
4.10　楕円ElGamal暗号（楕円曲線暗号）
4.11　IDベース暗号

●CHAPTER 5　ハッシュ関数
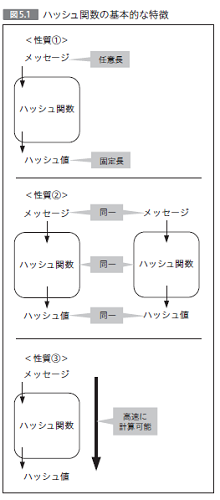
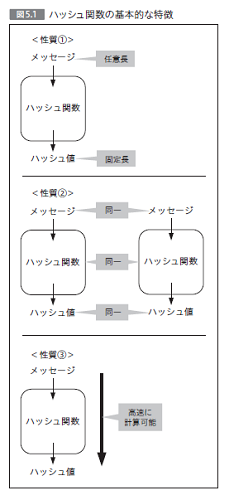
5.1　ハッシュ関数の概要
5.2　ハッシュ関数の安全性
5.3　ハッシュ関数の応用
5.4　ハッシュ関数の基本設計
5.5　反復型ハッシュ関数
5.6　代用的なハッシュ関数
5.7　ハッシュ関数への攻撃

●CHAPTER 6　メッセージ認証コード
6.1　メッセージ認証コードの概要
6.2　メッセージ認証コードの課題
6.3　メッセージ認証コードの安全性
6.4　CBC-MAC
6.5　EMAC
6.6　CMAC
6.7　HMAC
6.8　認証暗号

●CHAPTER 7　デジタル署名
7.1　デジタル署名の概要
7.2　デジタル署名の定義
7.3　デジタル署名と公開鍵暗号の関係
7.4　デジタル署名の安全性
7.5　デジタル署名に対する攻撃
7.6　RSA署名
7.7　RSA-FDH署名
7.8　ElGamal署名
7.9　Schnorr署名
7.10　DSA署名
7.11　その他の署名

●CHAPTER 8　鍵と乱数
8.1　鍵の配送
8.2　鍵管理
8.3　PKI（公開鍵基盤）
8.4　リポジトリ
8.5　電子証明書
8.6　乱数
8.7　疑似乱数生成器

●CHAPTER 9　その他の暗号トピック
9.1　ゼロ知識証明プロトコル
9.2　秘密分散共有法
9.3　電子透かし
9.4　SSL
9.5　OpenSSL
9.6　ビットコイン

【ダウンロード特典】
・エニグマ暗号
・じゃんけんプロトコル
・量子暗号
・S/MIME

会員特典はこちら

お問い合わせ

内容についてのお問い合わせは、正誤表、追加情報をご確認後に、お送りいただくようお願いいたします。

正誤表、追加情報に掲載されていない書籍内容へのお問い合わせや
その他書籍に関するお問い合わせは、書籍のお問い合わせフォームからお送りください。

利用許諾に関するお問い合わせ

本書の書影（表紙画像）をご利用になりたい場合は書影許諾申請フォームから申請をお願いいたします。
書影（表紙画像）以外のご利用については、こちらからお問い合わせください。

追加情報はありません。

ご購入いただいた書籍の種類を選択してください。

書籍の刷数を選択してください。

刷数は奥付（書籍の最終ページ）に記載されています。

現在表示されている正誤表の対象書籍

書籍の種類:

書籍の刷数:

本書に誤りまたは不十分な記述がありました。下記のとおり訂正し、お詫び申し上げます。

対象の書籍は正誤表がありません。

最終更新日:2024年02月13日
発生刷 ページ数 書籍改訂刷 電子書籍訂正 内容 登録日
1刷 002
「正誤表」と「刊行物Q&A」のURL		 5刷 済
誤 正誤表　http://www.shoeisha.co.jp/book/errata/ 刊行物Q&A　http://www.shoeisha.co.jp/book/qa/
正 正誤表　https://www.shoeisha.co.jp/book/errata/ 刊行物Q&A　https://www.shoeisha.co.jp/book/qa/
2021.06.18
1刷 032
下から5行目、シーザー暗号で暗号化した「book」の表記		 未 未
誤 bqqn / BQQN
正 brrn / BRRN
2024.02.13
1刷 033
上から1行目		 未 未
誤 "EQQN"→"bQQN"→"booN"→"book"
正 "ERRN"→"bRRN"→"booN"→"book"
2024.02.13
1刷 037
上から5行目（演習の暗号文の文字列）		 3刷 済
誤 暗号文 "YNRJKQNJXQNPJFSFWWTB"
正 暗号文 "KZDVWCZVJCZBVRERIIFN"
2017.10.16
1刷 050
上から9行目（箇条書き部分）		 未 未
誤 ・1番目の文字→3番目にする ・2番目の文字→1番目にする ・3番目の文字→4番目にする ・4番目の文字→2番目にする
正 ・（平文の）1番目の文字→（暗号文の）2番目にする ・（平文の）2番目の文字→（暗号文の）4番目にする ・（平文の）3番目の文字→（暗号文の）1番目にする ・（平文の）4番目の文字→（暗号文の）3番目にする
2022.07.21
1刷 092
上から5行目		 3刷 済
誤 つまり、任意のタイミングで暗号文オラクルに…
正 つまり、任意のタイミングで暗号化オラクルに…
備
考		 暗号文オラクル→暗号化オラクル
2017.09.13
1刷 105
問題　上から5行目		 5刷 済
誤 k=0の確率を1/2、
正 key=0の確率を1/2、
2021.02.02
1刷 146
図3.31		 5刷 済
誤 Sの添え字（S1）
正 左から順に、S1、S2、S3、S4、S5、S6、S7、S8
2020.04.21
1刷 149
表3.12　S7の2行15列目のセル		 5刷 済
誤 12
正 2
備
考		 12が重複してしまっていました。1行には各数字が1度だけ現れなければなりません。
2021.02.02
1刷 150
「問題」の2行目、3行目		 2刷 済
誤 （1）S1に01 0101bを入力したときの出力値を求めてください。 （2）S5に01 0101bを入力したときの出力値を求めてください。
正 （1）S1に01 1001bを入力したときの出力値を求めてください。 （2）S5に01 1001bを入力したときの出力値を求めてください。
2017.08.30
1刷 150
「解答」の1行目、5行目		 2刷 済
誤 （1）行番号：01b→1、列番号：1010b→12 （2）行番号：01b→1、列番号：1010b→12
正 （1）行番号：01b→1、列番号：1100b→12 （2）行番号：01b→1、列番号：1100b→12
2017.08.30
1刷 154
上から5行目		 未 未
誤 E(￣x)=PC1(￣x1,…,￣x32)=～
正 E(￣x)=E(￣x1,…,￣x32)=～
2022.05.18
1刷 156
13～15行目		 未 未
誤 = 0001111? 0001111? 0001111? 0001111? 1110000? 1110000? 1110000? 1110000?b
= 00011111 00011111 00011111 00011111 11100000 11100000 11100000 11100000b
= 0x1F1F 1F1F E0E0 E0E0
正 = 0001111? 0001111? 0001111? 0001111? 0000111? 0000111? 0000111? 0000111?b
= 00011111 00011111 00011111 00011111 00001110 00001110 00001110 00001110b
= 0x1F1F 1F1F 0E0E 0E0E
2021.12.27
1刷 156
18～20行目		 未 未
誤 = 1110000? 1110000? 1110000? 1110000? 0001111? 0001111? 0001111? 0001111?b
= 11100000 11100000 11100000 11100000 00011111 00011111 00011111 00011111b
=0xE0E0 E0E0 1F1F 1F1F
正 = 1110000? 1110000? 1110000? 1110000? 1111000? 1111000? 1111000? 1111000?b
= 11100000 11100000 11100000 11100000 11110001 11110001 11110001 11110001b
=0xE0E0 E0E0 F1F1 F1F1
2021.12.27
1刷 156
下から1～2行目		 未 未
誤 0x0101 0101 0101 0101, 0x1F1F 1F1F E0E0 E0E0,
0xE0E0 E0E0 1F1F 1F1F, 0xFEFE FEFE FEFE FEFE
正 0x0101 0101 0101 0101, 0x1F1F 1F1F 0E0E 0E0E,
0xE0E0 E0E0 F1F1 F1F1, 0xFEFE FEFE FEFE FEFE
2021.12.27
1刷 158
1行目～6行目		 未 未
誤 (0x01FE 01FE 01FE 01FE, 0xFE01 FE01 FE01 FE01)
(0x1FE0 1FE0 1FE0 1FE0, 0xE01F E01F E01F E01F)
(0x01E0 01E0 01E0 01E0, 0xE001 E001 E001 E001)
(0x1FFE 1FFE 1FFE 1FFE, 0xFE1F FE1F FE1F FE1F)
(0x011F 011F 011F 011F, 0x1F01 1F01 1F01 1F01)
(0xE0FE E0FE E0FE E0FE", 0xFEE0 FEE0 FEE0 FEE0)
正 (0x01FE 01FE 01FE 01FE, 0xFE01 FE01 FE01 FE01)
(0x1FE0 1FE0 0EF1 0EF1, 0xE01F E01F F10E F10E)
(0x01E0 01E0 01F1 01F1, 0xE001 E001 F101 F101)
(0x1FFE 1FFE 0EFE 0EFE, 0xFE1F FE1F FE0E FE0E)
(0x011F 011F 010E 010E, 0x1F01 1F01 0E01 0E01)
(0xE0FE E0FE F1FE F1FE, 0xFEE0 FEE0 FEF1 FEF1)
2021.12.27
1刷 168
「サブ鍵生成アルゴリズム」の動作の4の下から11行目		 4刷 済
誤 4c： j<4(i-1)の間、次の処理を繰り返します。
正 　4c： j<4 の間、次の処理を繰り返します。
2020.02.10
1刷 168
上から8行目（「動作」の1行目）		 3刷 済
誤 1：keyを1ワード（＝4バイト＝32バイト）…
正 1：keyを1ワード（＝4バイト＝32ビット）…
備
考		 32バイト→32ビット
2018.01.16
1刷 177
図3.44 1行目の4列目（左図、右図の2カ所とも）		 3刷 済
誤 s1,3
正 s0,3
2017.12.27
1刷 182
動作の3		 未 未
誤 i≠1の場合、～
正 i≠Nの場合、～
備
考		 ※iはNからスタート（デクリメントされる）し、その初回ラウンドではInvMixColumns処理を適用しません。
2022.05.30
1刷 235
表4.1　「選択暗号文攻撃」の行、「一方向性と強秘匿性」の間		 5刷 済
誤 OW-CCA1→IND-CCA1
正 OW-CCA1←IND-CCA1
備
考		 矢印の向きが逆
2021.02.02
1刷 246
上から3行目		 未 未
誤 greatest common devide
正 greatest common divisor
2021.08.23
1刷 250
「ユークリッドの互除法」の「動作」の3の2行目		 4刷 済
誤 除数nをmに、余りrをnに置き変えて
正 mにnを、nにrを入力して
2019.07.30
1刷 263
上から2行目		 未 未
誤 0～6の数が1つずつ登場しています。
正 0～5の数が1つずつ登場しています。
2023.01.27
1刷 268
破線枠の下から4行目		 3刷 済
誤 φ(24)
正 φ(30)
2017.12.27
1刷 268
破線枠の下から1行目		 3刷 済
誤 φ(24)
正 φ(30)
2017.12.27
1刷 268
上から2行目		 4刷 未
誤 φ(n)になっています。
正 φ(n)＝n－1になっています。
2019.04.12
1刷 271
下から6行目		 5刷 済
誤 256ビット（10進39桁）の合成数は、
正 256ビット（10進78桁）の合成数は、
2020.03.17
1刷 286
「共通法攻撃とは」上から5行目		 5刷 済
誤 pk=(N,di )、sk=ei
正 pk=(N,ei )、sk=di
2021.01.12
1刷 287
上から1行目		 4刷 済
誤 秘密鍵sk1＝d2
正 秘密鍵sk1＝d1
2019.04.12
1刷 297
「ゴードン（Gordon）の強素数生成アルゴリズム」の「動作」3		 4刷 済
誤 0.4kビットの素数を生成します。
正 0.4kビットの素数sを生成します。
2019.04.12
1刷 300
下から6行目		 3刷 済
誤 ……であるため、m＝21 mod 77になります。
正 ……であるため、m＝43 mod 77になります。
2018.03.05
1刷 300
下から5行目		 3刷 済
誤 c＝m^e＝21^3＝9261 mod 77＝21 mod77
正 c＝m^e＝43^3＝79507 mod 77＝43 mod 77
備
考		 「^」は上付き文字を表します。「m^e」はmのe乗、「43^3」は43の3乗。
2018.03.05
1刷 311
「Gaussのアルゴリズム」の「動作」3d		 4刷 済
誤 i＝i＋i
正 i＝i＋1
2019.04.12
1刷 312
「Garnerのアルゴリズム」の「動作」1		 4刷 済
誤 i＝2、b＝0とします。
正 i＝2とします。
2019.04.12
1刷 321
下から4行目		 4刷 済
誤 tを大きな素数として
正 qを大きな素数として
2019.03.25
1刷 349
図4.42　DDH問題を解くアルゴリズムの入出力		 5刷 済
誤
正
2021.02.02
1刷 353
上から11行目		 4刷 済
誤 c'＝(c_0,c_1・m')
正 c'＝(c_1,c_2・m')
備
考		 「_」は下付きを表しています。1と2は下付き文字となります。
2019.04.22
1刷 363
（vii）（相互法則）の式		 5刷 済
誤 (p = 1 mod 4 or q = 1 mod 4)
正 (m = 1 mod 4 or n = n mod 4)
2021.02.02
1刷 380
復号アルゴリズムの「動作」の1の1行目		 5刷 済
誤 f -1 (sk,x)を計算して、
正 f -1 (sk,c)を計算して、
2021.02.02
1刷 383
本文の下から6行目		 5刷 済
誤 「2048ビットの公開鍵であるElGamal暗号」と「256ビットの公開鍵である楕円ElGamal暗号」は同等の安全性を持ちます。
正 「3072ビットの公開鍵であるElGamal暗号」と「256ビットの公開鍵である楕円ElGamal暗号」は同等の安全性（128ビット安全性）を持ちます。
2021.02.02
1刷 383
本文の下から3行目		 5刷 済
誤 暗号文が4096ビットであれば、
正 暗号文が6144ビットであれば、
2021.02.02
1刷 385
上から4行目		 4刷 済
誤 Z_mが可換群であることは～
正 （Z_m,＋）が可換群であることは～
備
考		 「_」は下付きを表しています。mは下付き文字となります。
2019.04.22
1刷 389
上から1行目		 3刷 済
誤 よって、f2＝x2＋1、f4＝x2＋x＋1が、2次の既約多項式になります。
正 よって、f4＝x2＋x＋1が、2次の既約多項式になります。
備
考		 「f2＝x2＋1」を削除（既約多項式ではない）
2017.09.13
1刷 405
下から2行目		 4刷 済
誤 表4.53を参考
正 表4.55を参考
2019.04.22
1刷 420
図5.1　＜性質①＞と＜性質③＞ 		4刷 済
誤
正
備
考		 性質1と3の矢印の位置を変更しました。
2019.07.30
1刷 463
「6.2.2 再送攻撃」の1行目		 3刷 済
誤 リプライ攻撃
正 リプレイ攻撃
2017.10.10
1刷 466
注釈「*2」		 4刷 済
誤 ある定義域と地域を～
正 ある定義域と値域を～
2019.04.22
1刷 521
上から3行目		 4刷 済
誤 m＝m1・m2、σ＝σ1,σ2
正 m＝m1・m2 mod N、σ＝σ1・σ2 mod N
2019.04.22
1刷 521
上から11行目		 4刷 済
誤 σ^e＝(σ1,σ2)^e＝～
正 σ^e＝(σ1・σ2)^e＝～
2019.04.22
1刷 547
表7.4内、署名生成アルゴリズムで4カ所、署名検証アルゴリズムで2カ所		 未 未
誤 H(m,r)
正 H(m||r)
2022.11.29
1刷 548
図7.18　KeyGenの中		 5刷 済
誤
（画像クリックで拡大）
正
（画像クリックで拡大）
2020.07.27
1刷 549
鍵生成アルゴリズムの「動作」4		 5刷 済
誤 Zqからsをランダムに選び、y=gs mod pを計算します。
正 Zqからxをランダムに選び、y=gx mod pを計算します。
2020.07.27
1刷 549
鍵生成アルゴリズムの「動作」5		 5刷 済
誤 sk=sとして、
正 sk=xとして、
2020.07.27
1刷 549
注釈*22		 5刷 済
誤 y=g-s mod pになります。本書では解説上y=gs mod pとしています。
正 y=g-x mod pになります。本書では解説上y=gx mod pとしています。
2020.07.27
1刷 550
本文上から11行目		 5刷 済
誤 をy=g-s mod pとした方が好ましいといえます。
正 をy=g-x mod pとした方が好ましいといえます。
2020.07.27
1刷 583
上から4～5行目		 5刷 済
誤 224～255ビットの鍵長
正 256～383ビットの鍵長
2021.02.02
1刷 656
(k,n)しきい値法の［2］復元段階		 3刷 済
誤 2：f(x)が復元できれば～
正 3：f(x)が復元できれば～
備
考		 ※ステップ2が2つあったので、2つ目をステップ3に訂正します
2017.10.10
1刷 658
表9.1の上から4行目（x＝3）		 5刷 済
誤 f(3)＝～省略～＝51 mod 17＝10
正 f(3)＝～省略～＝61 mod 17＝10
2019.10.08
1刷 691
アドレス生成アルゴリズムの「動作」2		 5刷 済
誤 ハッシュ関数RIPEND-160にステップ1の結果を入力します。
正 ハッシュ関数RIPEMD-160にステップ1の結果を入力します。
備
考		 図9.24内の「RIPEND-160」も同様に修正します。
2020.07.03
1刷 700
表の上から11行目（左端の列、見出し行を除く）		 2刷 済
誤 (NL)
正 (LF)
備
考		 NL（＝New Line＝改行）からLF（＝Line Feed）に修正していますが、NLでも間違いではありません。多く見られる記述に合わせました。
2017.08.30
1刷 700
表の下から7行目（左端の列）		 2刷 済
誤 (Em)
正 (EM)
2017.08.30
1刷 718
右側の上から11行目		 3刷 済
誤 リプライ攻撃
正 リプレイ攻撃
2017.10.10

感想・レビュー

kaizen@名古屋de朝活読書会 さん

2017-09-18

#説明歌　暗号化攻撃手法と対にして守ると破る同じ比重で　機密性完全可用真正性信頼責任追跡安心　鍵配送ハッシュ関数メッセージ認証コードデジタル署名

masabi さん

2021-04-08

【概要】暗号技術の数学を含めて解説する。【感想】挫折した。

HANA さん

2017-11-26

IT関連の暗号技術について。内容としては結構広範囲に渡る内容でボリュームが凄い。ただそれぞれ考え方やそれに対する攻撃方法なんかも載っているので結構面白い。必要なだけ数式が載っているのも突き放されている感じがしなくて良かった。ただ1回読んだだけでは頭に入りきらなかったので何度か読まないとダメかも。

関連情報

​